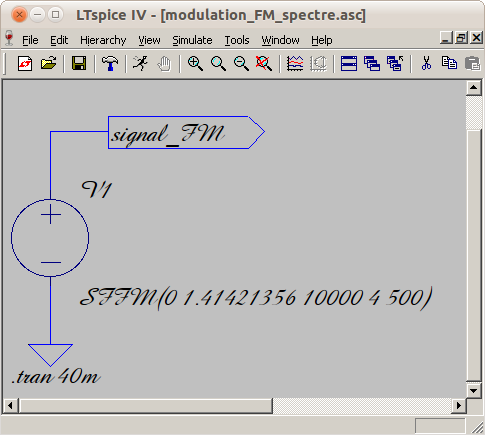
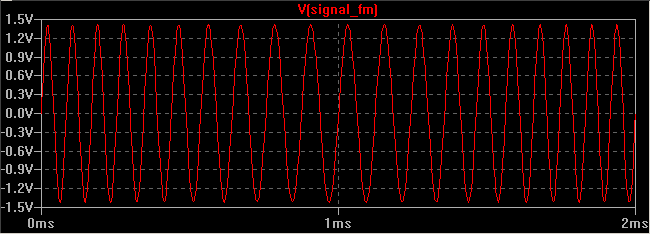

| fréquence | amplitude théorique (en mV efficace) |
amplitude obtenue par
simulation (en mV efficace) |
| 10 kHz | 397,14 | 393 |
| 9,5 et 10,5 kHz | 66,04 |
65,3 |
| 9 et 11 kHz | 364,12 |
361 |
| 8,5 et 11,5 kHz | 430,17 |
426 |
| 8 et 12 kHz | 281,12 | 278 |
| 7,5 et 12,5 kHz | 132,08 | 131 |
| 7 et 13 kHz | 49,08 | 48,6 |
| 6,5 et 13,5 kHz | 15,17 |
15,0 |
| 6 et 14 kHz | 4,028 | 4,0 |
| 5,5 et 14,5 kHz | 0,9386 | 0,93 |
| 5 et 15 kHz | 0,1950 | 0,19 |
| etc... | ... |
négligeable |
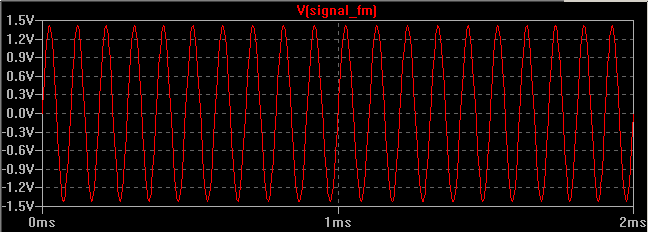
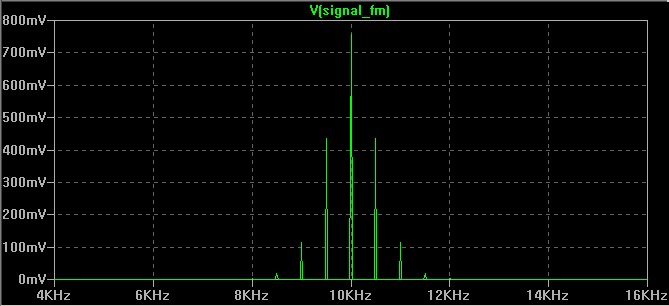
B = 2fm(m+1)