![]() Matlab
- Résolution d’équations différentielles
Matlab
- Résolution d’équations différentielles
ode23 : algorithme de Runge-Kutta du 2ème et 3ème ordres
ode45 : algorithme de Runge-Kutta du 4ème et 5ème ordres
Soit une fonction y1(t) soumise à l’équation différentielle :
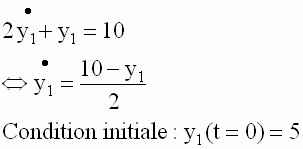
Créons le fichier f10.m :

>> [ t , y ] = ode23 ( 'f10' , 0 , 20 , [ 5 ] )
t =
0
0.1562
0.4833
...
18.0327
19.2827
20.0000
y =
5.0000
5.3758
6.0735
...
9.9995
9.9997
9.9998
>> plot ( t , y )
>> grid on
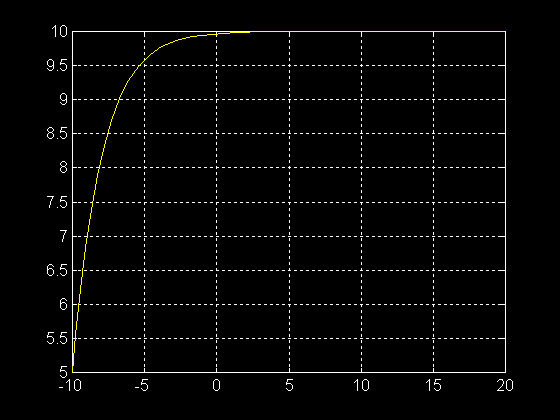
Pour avoir une tolérance sur les calculs de 1e-7 :
>> [ t , y ] = ode23 ('f10' , 0 , 20 , [ 5 ] , 1e-7)
A tester :
>> [t , y ] = ode45 ( 'f10' , 0 , 20 , [ 5 ] )

Créons le fichier f11.m :

>> [ t , y ]=ode23 ( 'f11' , 0 , 10 , [ 0 2 ] )
t =
0
0.0781
0.1858
...
9.7555
9.9671
10.0000
y =
0 2.0000
-0.3058 1.9880
-0.7017 1.9334
...
-0.2114 0.1188
-0.2284 0.0719
-0.2291 0.0644
>> plot ( t , y )

Pour n'afficher que la première colonne, c'est-à-dire y1(t) ou dy2(t)/dt :
>> plot ( t , y ( : , 1 ) )
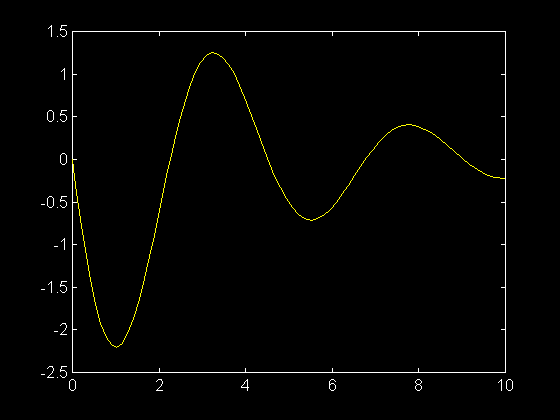
Pour n'afficher que la deuxième colonne, c'est-à-dire y2(t) :
>> plot ( t , y ( : , 2 ) )
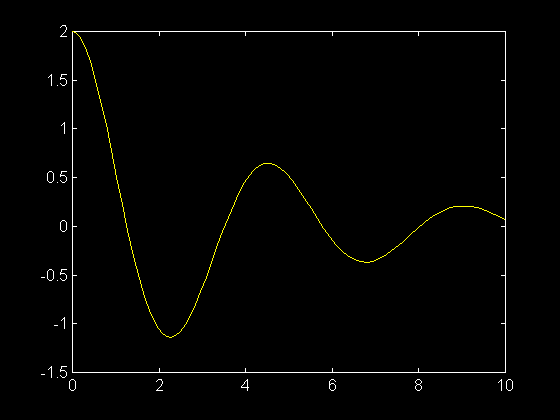
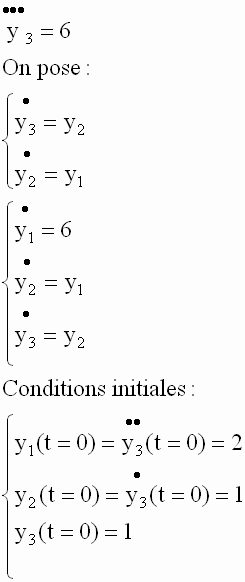
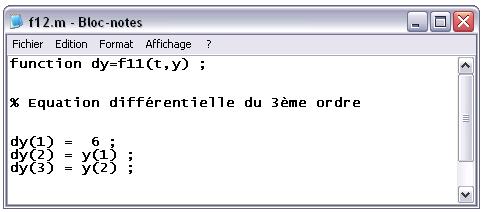
Créons le fichier f12.m :
>> [ t , y ] = ode23 ( 'f12' , 0 , 2 , [ 2 1 1 ] )
t =
0
0.0156
0.1290
...
1.8692
1.9942
2.0000
y =
2.0000 1.0000 1.0000
2.0938 1.0320 1.0159
2.7741 1.3080 1.1478
...
13.2149 15.2195 12.8932
13.9649 16.9183 14.9009
14.0000 17.0000 15.0000
>> plot ( t , y )
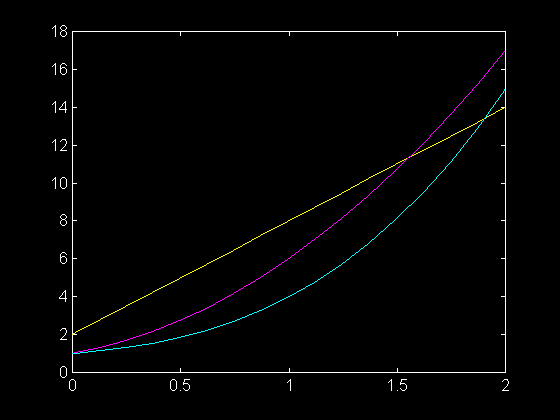
Pour n'afficher que la troisième colonne, c'est-à-dire y3(t) :
>> plot ( t , y ( : , 3 ) )
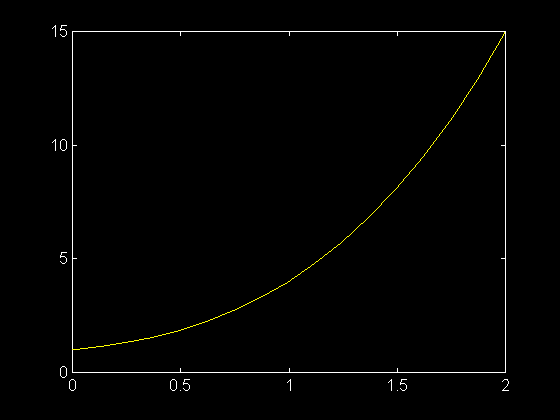
Nous allons comparer avec la solution exacte : y3(t) = t^3 + t^2 + t + 1
>> hold on
>> fplot ( 'x^3 + x^2 + x + 1 ' , [ 0 2 ] , 'b--' )
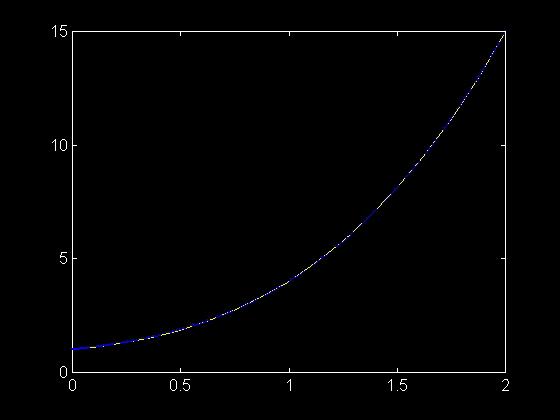
Les deux courbes sont superposées.
Equation de Van der Pol
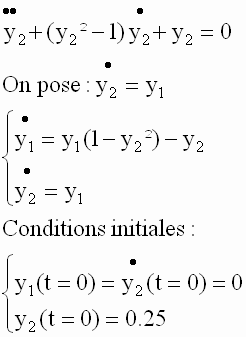
Créons le fichier f9.m :

>> [ t , y ]=ode23 ( 'f9' , 0 , 20 , [ 0 0.25 ] )
>> plot ( t , y )

© Fabrice Sincère