![]() Matlab
- Graphe en deux dimensions
Matlab
- Graphe en deux dimensions
|
plot
|
trace point par point un graphe 2D
|
|
semilogx
|
identique à plot mais avec
échelle logarithmique pour l'axe des abscisses
|
|
semilogy
|
identique à plot mais avec
échelle logarithmique pour l'axe des ordonnées
|
|
loglog
|
identique à plot mais avec
échelles logarithmiques pour les deux axes
|
|
grid
|
ajoute une grille
|
|
xlabel
|
ajoute une légende pour l'axe des
abscisses
|
|
ylabel
|
ajoute une légende pour l'axe des
ordonnées
|
|
title
|
ajoute un titre
|
|
axis
|
modifie les échelles des axes
|
|
zoom
|
effectue un zoom
|
|
gtext
|
place une légende avec la souris
|
|
hold
|
ajoute un graphe dans la fenêtre
courante
|
|
figure
|
crée une nouvelle fenêtre
|
|
Temps (heures) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
|
Température (°C) |
20 |
23 |
30 |
33 |
32 |
37 |
34 |
39 |
36 |
>> temps = [0 2 4 6 8 10 12 14 16]
temps =
0 2 4 6 8 10 12 14 16
>> temperature = [20 23 30 33 32 37 34 39 36]
temperature =
20 23 30 33 32 37 34 39 36
>> plot (temps , temperature)
>> grid on
>> xlabel ( 'temps (en heures)' )
>> ylabel ( 'température (en °C)' )
>> title ( 'Suivi de température' )
>> axis ( [ 0 18 10 40 ] )
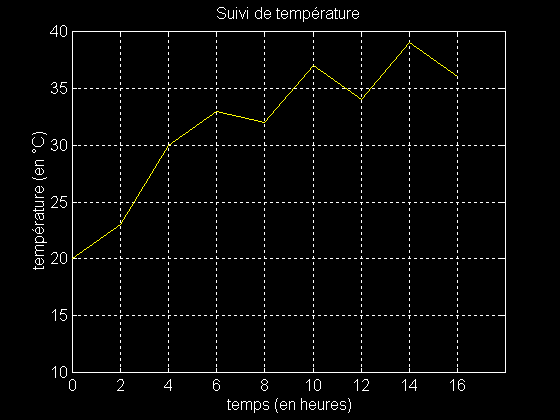
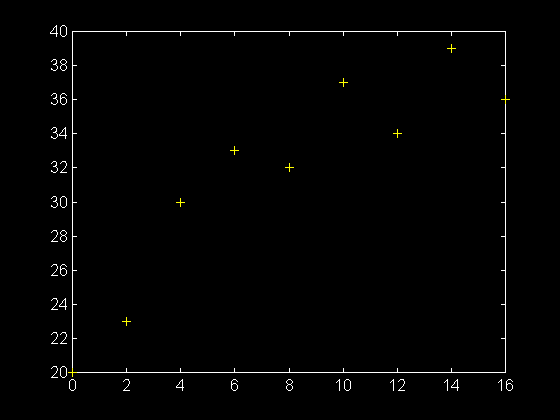
>> plot ( temps , temperature ,'+' )
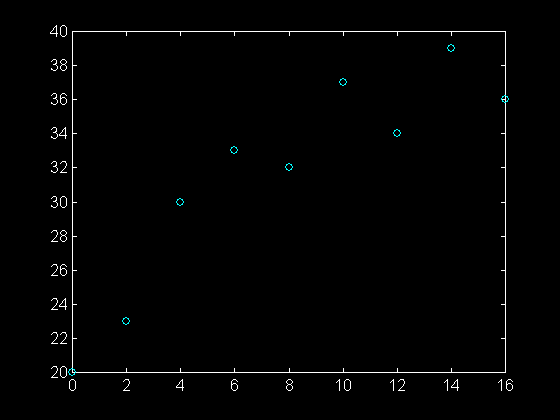
>> plot ( temps , temperature , 'co' )
>> plot ( temps , temperature , ':' )
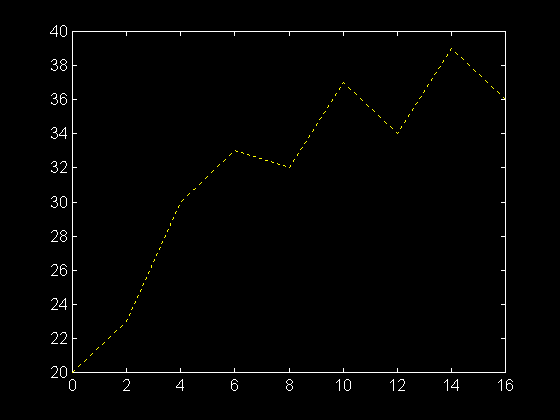
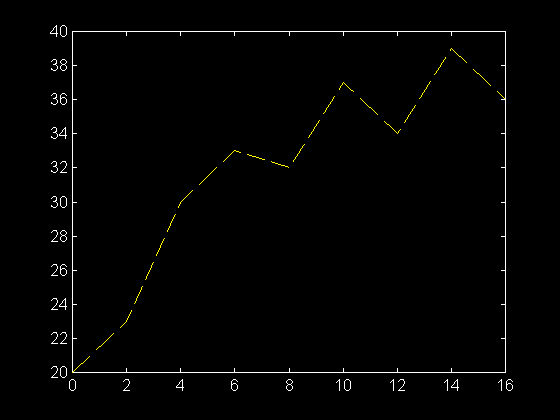
>> plot ( temps , temperature , '--' )
Autres options :
|
y |
Jaune |
|
m |
Magenta |
|
c |
Cyan |
|
r |
Rouge |
|
g |
Vert |
|
b |
Bleu |
|
w |
Blanc |
|
k |
Noir |
|
. |
|
o |
|
x |
|
+ |
|
- |
|
* |
|
: |
|
-. |
|
-- |
![]()
Création du vecteur t :
>> t = 0 : 0.01 : 1
t =
Columns 1 through 7
0 0.0100 0.0200 0.0300 0.0400 0.0500 0.0600
…
Columns 99 through 101
0.9800 0.9900 1.0000
Création du vecteur y :
Attention : ne pas oublier le point devant les opérateurs multiplication, puissance et division :
.*
.^
./
>> y = t.*(1 + t.^2)./10
y =
Columns 1 through 7
0 0.0010 0.0020 0.0030 0.0040 0.0050 0.0060
…
Columns 99 through 101
0.1921 0.1960 0.2000
>> plot ( t , y )
>> grid on

Remarque : il est plus efficace d’utiliser la fonction fplot
x = 4cos(t)
y = sin(t)
>> t = 0 : pi/100 : 2*pi
>> x = 4*cos(t)
>> y = sin(t)
>> plot ( x , y )

© Fabrice Sincère