Diagramme de Bode
Log10 : logarithme décimal
Semilogx : identique à la fonction plot mais avec une échelle logarithmique pour l’axe des abscisses
Loglog : identique à la fonction plot mais avec une échelle logarithmique pour l’axe des abscisses et des ordonnées
Considérons un filtre passe-bas du 2ème ordre, de fonction de transfert :
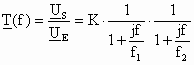
avec : K = 10, f1 = 1 kHz et f2 = 10 kHz.
Il faut commencer par créer le fichier t4.m de la fonction de transfert :
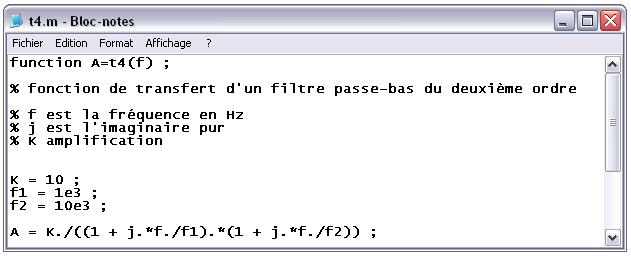
Valeur de la fonction de transfert pour f = 0 Hz (régime continu) :
>> t4(0)
ans =
10
Valeur de la fonction de transfert pour f = 100 Hz :
>> t4(100)
ans =
9.8901 - 1.0890i
Le module donne l'amplification :
>> abs(t4(100))
ans =
9.9499
L'argument donne le déphasage (en radians) :
>> angle(t4(100))
ans =
-0.1097
Etudions la fonction de transfert sur la gamme de fréquence 100 Hz à 100 kHz :
>> log10(100)
ans =
2
>> log10(100000)
ans =
5
Nous allons créer un vecteur logf :
>> logf = 2 : 0.01 : 5
>> f = 10.^logf
f est un vecteur qui nous donne 300 points uniformément répartis de 100 Hz à 100 kHz (compte tenu de l’échelle logarithmique).
G est un vecteur qui nous retourne le gain (en dB) pour les fréquences précédentes :
>> G = 20.*log10 (abs (t4(f)) )
>> semilogx ( f , G )
>> ylabel ( 'gain (dB)' )
>> xlabel ( 'fréquence (Hz)' )
>> title ( 'diagramme de Bode du gain' )
>> grid on
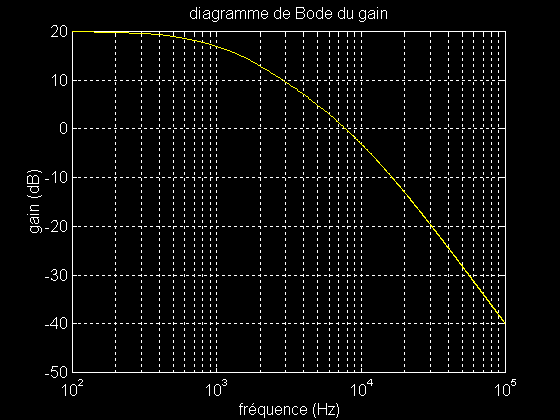
Déphasage en degrés :
>> dephasage = angle(t4(f))*180/pi
>> semilogx ( f , dephasage )
>> grid on

![]()
Fichier de définition de la fonction t2 :
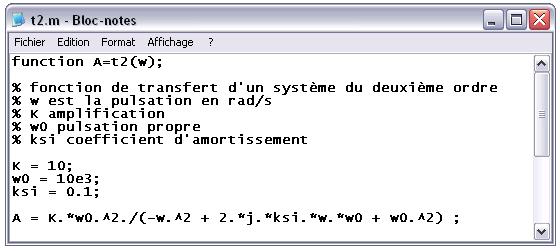
>> logpulsation = 3 : 0.01 : 6
>> pulsation = 10.^logpulsation
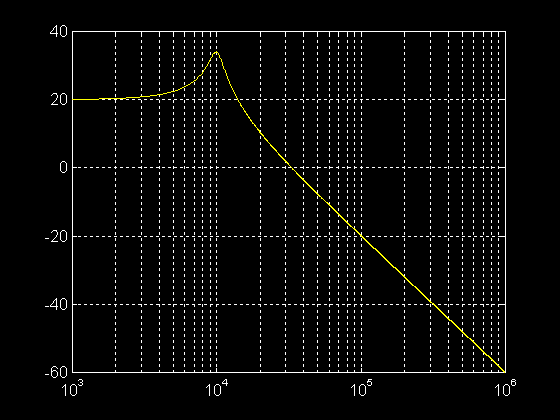
>> G = 20.*log10(abs(t2(pulsation)))
>> semilogx ( pulsation , G )
>> grid on
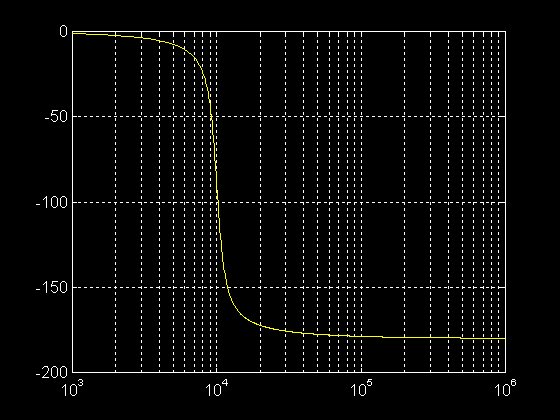
>> dephasage = angle(t2(pulsation))*180/pi
>> semilogx ( pulsation , dephasage )
>> grid on
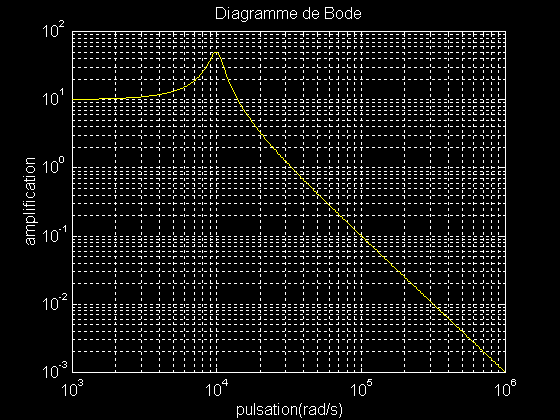
>> amplification = abs(t2(pulsation))
>> loglog ( pulsation , amplification)
>> grid on
>> xlabel ( 'pulsation(rad/s)' )
>> ylabel ( 'amplification' )
>> title ( 'Diagramme de Bode' )
© Fabrice Sincère